LAB SESSION 3

NUMERICAL PRESENTATION OF UNIVARIATE DATA

INTRODUCTION: The basic idea of descriptive statistics is to describe a set of data in a variety of abbreviated ways. In this lab you will investigate measures of central tendency and dispersion. The box-and-whiskers display, a graphical display of the 5-number summary of a set of data, will also be introduced.

MEASURES OF CENTRAL TENDENCY AND DISPERSION

Measures of central tendency and variation are the foundation of descriptive statistics but most of these formulas are quite tedious to compute, even with a calculator. Fortunately, we can find a number of commonly used descriptive statistics using just a single command. Enter the data in Exercise 2.66 into column A.

Get a histogram of your data and visually approximate the "center".

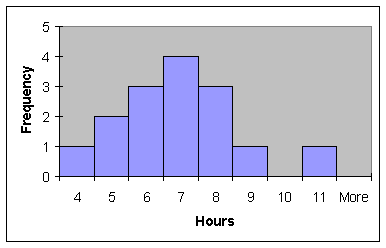
Calculate the mean (and median) using the following commands.

Activate a cell for the answer, then continue with:

Choose: Insert function, f_x > Statistical > AVERAGE (or MEDIAN)> OK

Enter: Number 1: (A2:A16 or select cells)

mean	median
6.933333	7

We can also compute the midrange by using the statistical functions MAX and

MIN as follows:

select a cell to hold the result, then click in the formula box and type (selecting

the appropriate statistical function - shown in bold)

.5*(MAX(A1:A15)+MIN(A1:A15))

midrange

7.5

Visually locate the three calculated centers on the histogram. Notice the three measures of central tendency are approximately the same. How well did you visually approximate the center?

Now, place the values of hours of sleep (column A) plus 4 into column B, do a histogram, visually locate the 'center', then determine the mean, median and midrange.

mean

10.93333

median

11

midrange

11.5

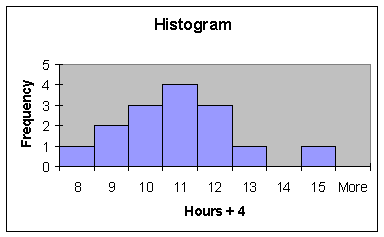
How did the three measures of central tendency (mean, median, and midrange) change?

Next, place the values of column A times 3 into column C, and follow the procedure above.

mean

20.8

median

21

midrange

22.5

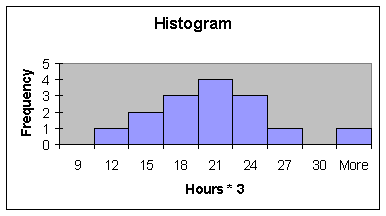
Compare the three measures of central tendency for the columns of data A, B and C. How and why did a change in the measures occur? If a different transformation was performed (such as dividing each entry in A by 2) could you make an educated guess about the effect on these three measures?

Consider Exercise 2.61 in the text. Retrieve the data (App02-02), do a histogram and calculate the mean, median and midrange. What is there about the distribution of these ten data values that causes these three averages to be so different?

mean

35400

median

33375

midrange

39750

mode

31500

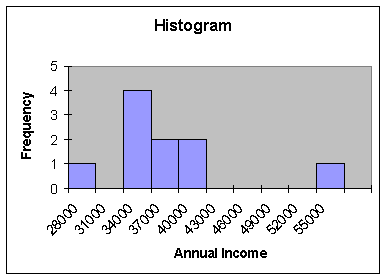
Compare the standard deviations for each of the previous four examples, along with how similar or how different the three measures of central tendency were. Can we use the standard deviation to predict whether we expect these three measures of central tendency to be quite similar or quite different?

FREQUENCY DISTRIBUTIONS

When the sample data are in the form of a frequency distribution, we can still use Excel to describe the distribution. The class marks need to be listed in one column with the corresponding frequencies in another. Start a new Excel workbook. (Choose: File > New > Workbook), and enter the following information, where X represents the number of radios in a household and Frequency is the number of households having X radios:

X Freq

1 20

2 35

3 100

4 90

5 65

6 40

7 5

Name column A as Radios, and B as Frequency. Create column C to be x*f and

D to be x²*f as follows:

Activate C2

Enter: =A2*B2

Drag: Bottom right corner of C2 down to give other products

Activate D2 and repeat above commands replacing the formula with =A2*C2

Activate the data in columns B, C and D.

Choose: AutoSum

To find mean, activate E2, then continue with:

Enter: =(C9/B9)

To find the variance, activate E3, then continue with:

Enter: =(D9-(C9^2/B9))/(B9-1)

To find the standard deviation, activate E4, the continue with:

Enter: =SQRT(E3)

*Reminder: in the case of a grouped frequency distribution enter the class marks in one column and the corresponding frequencies in another.

BOX-AND-WHISKER DISPLAY

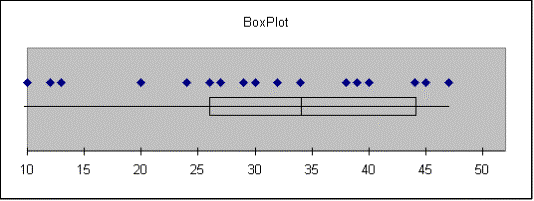
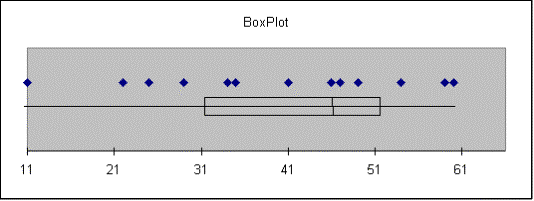
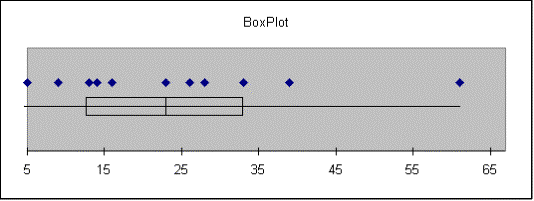
The boxplot (Excel's name for the box-and-whisker display) is a simple graph that gives a graphic 5-number summary. Information about the center, dispersion, and skewness of a data set will be illustrated. Retrieve the data for Exercise 2.18 (EX02-018) and construct a boxplot for each of columns A, B and C (Aaron, Ruth and Maris).

Choose: Tools > Data Analysis Plus > BoxPlot > OK

Enter: A2:A24 or select cells > OK

Aaron

Smallest = 10

Q1 = 26

Median = 34

Q3 = 44

Largest = 47

IQR = 18

Outliers:

Ruth

Smallest = 11

Q1 = 31.5

Median = 46

Q3 = 51.5

Largest = 60

IQR = 20

Outliers:

Maris

Smallest = 5

Q1 = 13

Median = 23

Q3 = 33

Largest = 61

IQR = 20

Outliers:

A rectangle is constructed between the two quartiles, with a line across the box indicating the location of the median. The box encloses the middle half of the data. The whiskers extend in either direction to indicate the maximum and minimum values.

Although “side-by-side” BoxPlots cannot be constructed in Excel, we can generate BoxPlots with the same scale for better comparison of the distributions. Activate all of columns A, B and C, then

Choose: Tools > Data Analysis Plus > Box Plot > OK > OK

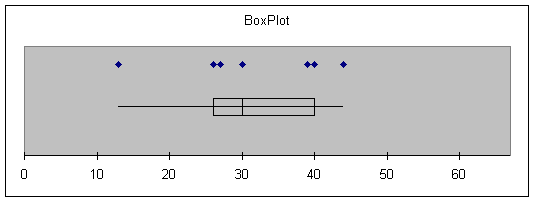
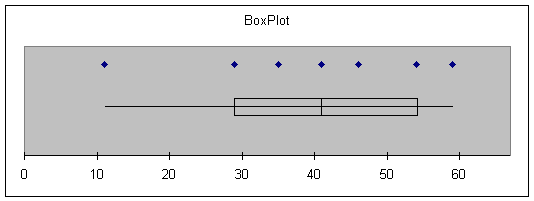
Consider again the salary data presented in Application 2 - 2. Retrieve the data from the Student Suite CD and perform a BoxPlot of the data in column A.

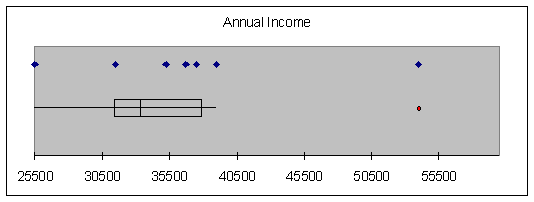
The red oval in the boxplot indicates an outlier- a data value that is far removed from the rest of the data.

ASSIGNMENT: