LAB SESSION 8

SAMPLE VARIABILITY

INTRODUCTION: In an effort to predict population parameters, we need to investigate the variability in the sample means obtained from repeated sampling. The Central Limit Theorem tells us that the sampling distribution of sample means, , is approximately normally distributed. In the following lab you will test the results of the Central Limit Theorem.

GENERATING THE DISTRIBUTIONS OF SAMPLE MEANS

Uniform Distribution

Enter the values 0 through 9 into column A and name column A 'X':

Enter the probabilities into column B. For the uniform distribution assign probabilities of .1 to the x-values 0 through 9. Name column 2 'UNIFORM':

Generate 30 sets of 100 uniform deviates (random numbers with a uniform distribution) and store them in columns F through AI.

(Reminder: Tools > Data Analysis > Random Number Generation > OK

Number of Variables: 30

Number of Random Numbers: 100

Distribution: Discrete

Value and Probability Input Range: A2:B11

Output Range: F2

Observe the distribution of the data in AI.

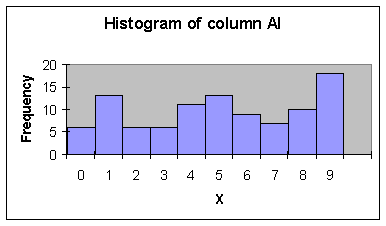
To illustrate the concept of a sampling distribution we're considering the finite population {0, 1, 2, ..., 9}. We shall generate values from three very different distributions and investigate, empirically, sampling distributions of the sample means,, for samples of size n=2, n=5, and n=30 for each of the different distributions.

(N=2) Calculate the sample mean, , for each pair of values given in columns F and G and store in column AJ:

Observe the distribution of the sample means in column AJ: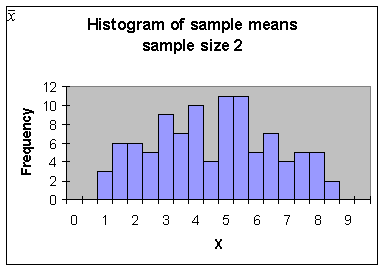

Notice that this distribution of sample means does not look like the population.

(N=5) Calculate for the values in H through L, storing your results in AK, then observe the distribution of the sample means in AK.

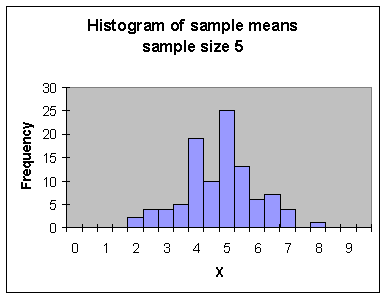
(N=30) Repeat the above procedure for the values in columns F through AJ, storing your results in AL.

Compare the descriptive statistics and distributions for each of the calculated means

		Distribution of sample mean
sample size 2		Sample size 5		Sample size 30

Mean	4.375	Mean	4.604	Mean	4.498667
Standard Deviation	1.73987	Standard Deviation	1.255285	Standard Deviation	0.460905
Range	8	Range	6.2	Range	1.966667
Minimum	0.5	Minimum	1.2	Minimum	3.6
Maximum	8.5	Maximum	7.4	Maximum	5.566667

Now, look at the distribution of sample means for samples of size 1(column F), size 2 (column AJ), size 5 (column AK), and size 30 (column AL) graphically (using the same scale for each):

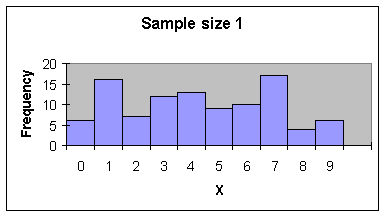
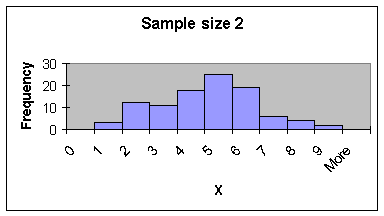
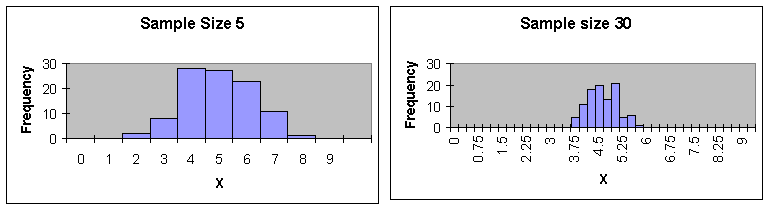
Note the shape of each of the distributions of the sample means. These distributions don't look like the original data (F), but they do have a shape we're familiar with.