LAB SESSION 9
ESTIMATION AND
HYPOTHESIS TESTING
INTRODUCTION: Two indispensable
statistical decision-making tools for a single parameter are (i)confidence
intervals, and (ii) hypothesis tests to investigate theories about
parameters.† In this lab you will learn
how to calculate confidence intervals and perform hypothesis tests (assuming we
know sigma) using Excel.
CONFIDENCE INTERVALS
††††††††††† As an introduction, letís follow Illustration
8.3 in your text.
Begin a new worksheet and generate 40 random
integers the range 0 to 9 in column A.†
You can use either the Random Numbers Table (Table 1) or the Random
Number Generation tool of Excel and then use the INT (integer) function to
transform to integers in the range 0 to 9:
††††††††††† Choose:† Tools > Data Analysis Plus > Random
Number Generation > OK
††††††††††† Enter:††††† Number of Variables: 1
††††††††††† †††††††††††††† Number of Random Numbers:† 40
††††††††††† Select:†††† Distribution:† Uniform
††††††††††† Enter:††††† Parameters, Between†† 0†† and††
9†
††††††††††††††††††††††† †† Output Range:†† B1† ††> OK
††††††††††† Enter:†††† in cell A1:† =INT(B1)
††††††††††† Click and drag: lower right corner to cell
A40
To see the mean, standard deviation and maximum and
minimum values for the data set use:
††††††††††† Select:† Tools > Data Analysis > Descriptive
Statistics > OK
††††††††††† enter input and output range
as appropriate, and select Summary Statistics
|
Column1 |
|
|
|
|
|
Mean |
3.9 |
|
Standard Error |
0.446927 |
|
Median |
3 |
|
Mode |
3 |
|
Standard Deviation |
2.826613 |
|
Sample Variance |
7.989744 |
|
Range |
8 |
|
Minimum |
0 |
|
Maximum |
8 |
|
Sum |
156 |
|
Count |
40 |
(Your
results may be slightly different, since we are using random data.)
Find the 90% confidence
interval for the mean of these values:
††††††††††† Choose:† Tools > Data Analysis Plus >
Z-Estimate: Mean > OK
††††††††††† Enter:†† †† Input Range:† A1:A40
††††††††††††††††††††††† †† Standard Deviation (SIGMA): 2.87 > OK
††††††††††† ††††††††††† †† Alpha :†
.10 > OK
|
z-Estimate: Mean |
|
|
|
|
|
|
|
|
|
Column 1 |
|
Mean |
|
4.9412 |
|
Standard Deviation |
2.6094 |
|
|
Observations |
17 |
|
|
SIGMA |
|
2.87 |
|
LCL |
|
3.796232 |
|
UCL |
|
6.086121 |
So the 90% confidence
interval for the mean is 3.80 to 6.09.
Find the 95% and 99%
confidence intervals for the mean of this same set of data and record the
results.
Looking at these three
intervals
1.†† Consider the
means obtained from 100 samples of size 40.†
If these means were used to construct 100 confidence intervals,
determine the expected number of times the population mean would be included in
one of these intervals.
2.†† In the 99%
confidence interval that you found, the level of significance is† 99%.†
What is the value of a ?† What does a† represent?
3.†† In which of
these intervals is the maximum error, E, the smallest?† What does this mean?† In which of these intervals are you being
more certain to include the population mean?
HYPOTHESIS
TESTING
A standard final examination
in an elementary statistics course is designed to produce a mean score of 75
and a standard deviation of 12.† The
hypothesis you will try to verify is: "This particular statistics class is
above average."† At the .05 level
of significance, test the claim that the following sample scores reflect an
above-average class (assuming sigma = 12):
79†† 79†† 78†† 74††
82†† 89†† 74†† 75†† 78††
73
74†† 84†† 82†† 66††
84†† 82†† 82†† 71†† 72††
83
Enter the data and get a
preliminary graphical analysis.
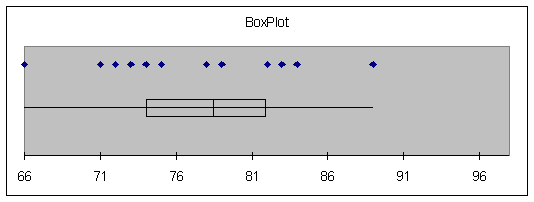
|
Column1 |
|
|
|
|
|
Mean |
78.05 |
|
Standard Error |
1.251263 |
|
Median |
78.5 |
|
Mode |
82 |
|
Standard Deviation |
5.595816 |
|
Sample Variance |
31.31316 |
|
Range |
23 |
|
Minimum |
66 |
|
Maximum |
89 |
|
Sum |
1561 |
|
Count |
20 |
Test the hypothesis,
"The mean test grade for this class is greater than 75."
††††††††††††††††† Choose:† Tools
> Data Analysis Plus > Z-Test: Mean > OK
††††††††††††††††† Enter:†††††
Input Range:† A1:A20 or select
cells > OK
††††††††††††††††††††††† †††††††††
Hypothesized
mean:† 75
††††††††††††††††††††††† †††††††††
Standard
Deviation (SIGMA):† 12† > OK
††††††††††††††††††††††† †††††††††
Alpha:† .05 > OK
The results are as follows:
|
Z-Test: Mean |
|
|
|
|
|
|
|
|
|
|
|
|
Column 1 |
|
Mean |
|
|
78.05 |
|
Standard Deviation |
|
5.5958 |
|
|
Observations |
|
20 |
|
|
Hypothesized Mean |
|
75 |
|
|
SIGMA |
|
|
12 |
|
z Stat |
|
|
1.1367 |
|
P(Z<=z) one-tail |
|
0.1278 |
|
|
z Critical one-tail |
|
1.6449 |
|
|
P(Z<=z) two-tail |
|
0.2556 |
|
|
z Critical two-tail |
|
1.96 |
|
Note that the p-values and
critical values for both one-tail and two-tail tests are given.
Questions:
1.†† What are the formal null and alternative hypotheses?
2.†† What is the value of the test statistic, and what is your
decision?† Is the mean of this class
above ďaverageĒ?
ASSIGNMENT: Do Exercises 8.30, and 8.129 in your text, and the following two
problems.
1.†† In one region of a city, a random survey of households includes a
question about the number of people in the household.† The results are given in the accompanying frequency table.† Construct the 90% confidence interval for
the mean size of all such households.†
Assume that the sample standard deviation can be used as an estimate of
the population standard deviation.
Household size†† ††††††††† †††1†††††
2††††† 3††††††† 4†††††
5†††† 6†††† 7††† †† †††††
Frequency††††††††††††††††††† 15†††† 20†††
37†††† 23†††† 14†††
4†††† 2
2.†† An aeronautical research team collects data on the stall speeds
(in knots) of ultralight aircraft.† The
results are summarized in the accompanying stem-and-leaf plot.† Construct the 95% confidence interval for
the mean stall speed of all such aircraft.†
Assume sigma = 1.
MTB
> Stem-and-Leaf c1.
Stem-and-leaf
of C1††††††† N† = 16
Leaf
Unit = 0.10
†††††††††††††††††† ††
†††††††††† †††††† †21. | 7 8
†††††† 22. | 3 4 4 6
†††††† 23. | 2 2 5 8 9 9
†††††† 24. | 0 1 3
†††††† †††† †††††††25. | 2